Behaviors

Each subsystem realizes one or multiple behaviors. The behavior switching is governed by a Finite State Machine (FSM), so that one behavior is executed in one state of the FSM.

velma_core_ve_body

FSM of velma_core_ve_body subsystem:

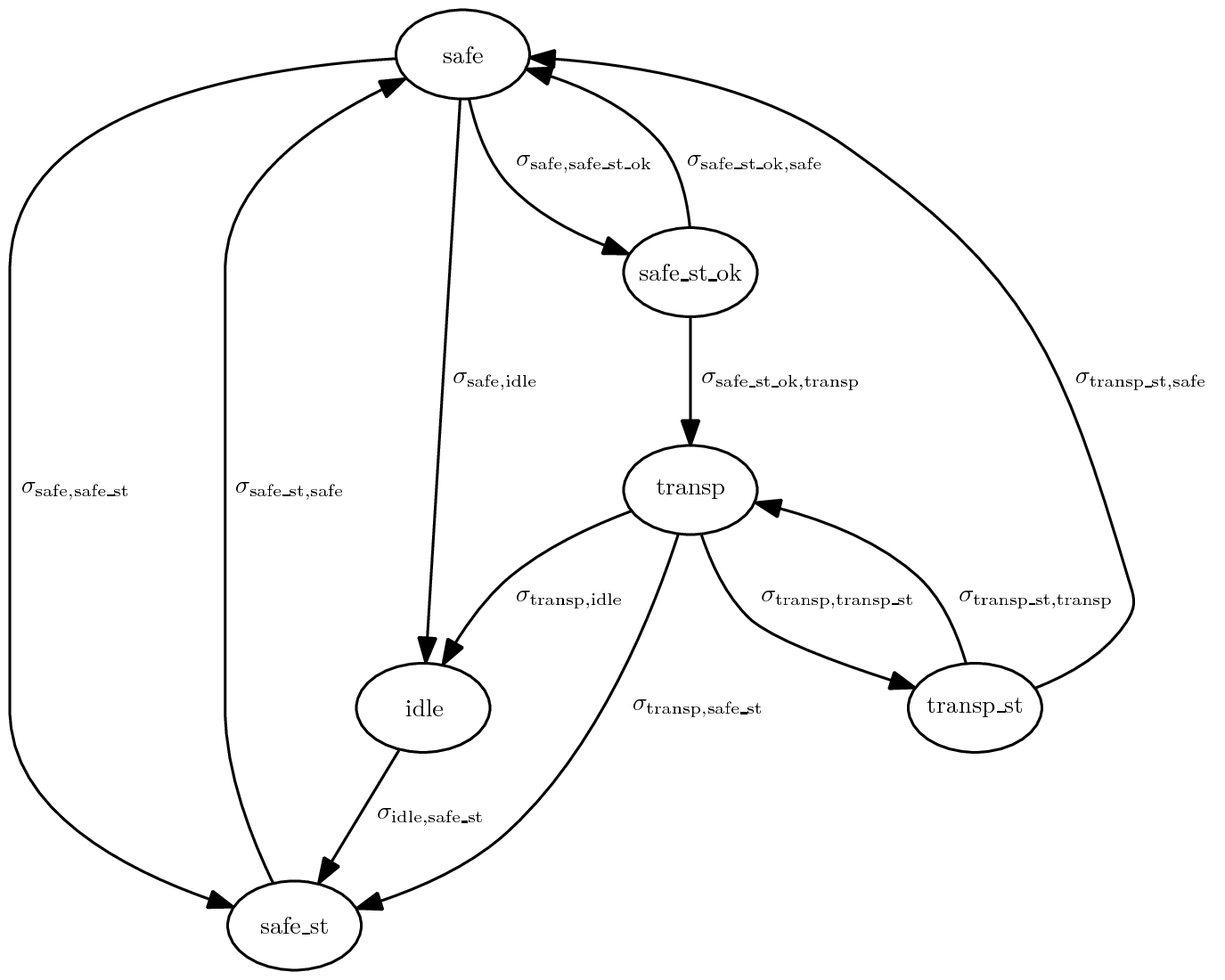
All states, except idle last exactly one iteration, so their terminal conditions are:

\[\scriptsize \tau_{\texttt{safe}} = \tau_{\texttt{safe_st}} = \tau_{\texttt{safe_st_ok}} = \tau_{\texttt{transp}} = \tau_{\texttt{transp_st}} = \texttt{TRUE}\]

The only state that can last for more than one iteration is idle, and its terminal condition is \(\scriptsize \tau_{\texttt{idle}} = \texttt{recvStatus}\), so the FSM is switched to safe_st upon successful reception of status data from real effectors: \(\scriptsize \sigma_{\texttt{idle},\texttt{safe_st}} = \texttt{TRUE}\). The state idle is the initial state.

Only one transition is possible from state safe_st, i.e. \(\scriptsize \sigma_{\texttt{safe_st},\texttt{safe}} = \texttt{TRUE}\).

The transition conditions for state safe are:

\[\scriptsize \sigma_{\texttt{safe},\texttt{safe_st}} = \texttt{recvStatus} \wedge \neg \texttt{allHwOk}\] \[\scriptsize \sigma_{\texttt{safe},\texttt{safe_st_ok}} = \texttt{recvStatus} \wedge \texttt{allHwOk}\] \[\scriptsize \sigma_{\texttt{safe},\texttt{idle}} = \neg \texttt{recvStatus}\]

The transition conditions for state safe_st_ok are defined as:

\[\scriptsize \sigma_{\texttt{safe_st_ok},\texttt{safe}} = \neg \texttt{recvCommand} \vee \neg \texttt{allCmdOk} \vee \neg \texttt{cmdExitSafeState} \vee \neg \texttt{safeItPassed500}\] \[\scriptsize \sigma_{\texttt{safe_st_ok},\texttt{transp}} = \texttt{recvCommand} \wedge \texttt{allCmdOk} \wedge \texttt{cmdExitSafeState} \wedge \texttt{safeItPassed500}\]

For state transp one transition is chosen using conditions:

\[\scriptsize \sigma_{\texttt{transp},\texttt{safe_st}} = \texttt{recvStatus} \wedge \neg \texttt{allHwOk}\] \[\scriptsize \sigma_{\texttt{transp},\texttt{transp_st}} = \texttt{recvStatus} \wedge \texttt{allHwOk}\] \[\scriptsize \sigma_{\texttt{transp},\texttt{idle}} = \neg \texttt{recvStatus}\]

The transition conditions for state transp_st are:

\[\scriptsize \sigma_{\texttt{transp_st},\texttt{transp}} = \texttt{recvCommand} \wedge \texttt{allCmdOk}\] \[\scriptsize \sigma_{\texttt{transp_st},\texttt{safe}} = \neg \texttt{recvCommand} \vee \neg \texttt{allCmdOk}\]

As error handling in this subsystem is not supported, error conditions for all states are defined as:

\[\scriptsize \epsilon_{\texttt{safe}} = \epsilon_{\texttt{safe_st}} = \epsilon_{\texttt{transp}} = \epsilon_{\texttt{transp_st}} = \epsilon_{\texttt{idle}} = \epsilon_{\texttt{safe_st_ok}} = \texttt{FALSE}\]

With predicates defined as:

• \(\scriptsize \texttt{recvStatus}\) - new status data was received from real effectors,
• \(\scriptsize \texttt{recvCommand}\) - new command data was received from velma_core_cs,
• \(\scriptsize \texttt{safeItPassed500}\) - the current number of non-interrupted iterations in state safe or safe_st or safe_st_ok is over 500,
• \(\scriptsize \texttt{cmdExitSafeState}\) - new command was received from velma_core_cs: exit safe state
• \(\scriptsize \texttt{allHwOk} = \texttt{rLwrOk} \wedge \texttt{lLwrOk} \wedge \texttt{rLwrInCmdState} \wedge \texttt{lLwrInCmdState} \wedge \texttt{tMotorOk} \wedge \texttt{hpMotorOk} \wedge \texttt{htMotorOk}\) - all real effectors are working properly
• \(\scriptsize \texttt{allCmdOk} = \texttt{rLwrCmdOk} \wedge \texttt{lLwrCmdOk} \wedge \texttt{tCmdOk}\) - all received commands are valid

As most of terminal conditions are always satisfied, state transitions in this subsystem happen usually on every iteration. The only exception is idle state, which can last longer than on iteration. Although the FSM and transition conditions seem complicated, the principle of operation is quite simple:

• if any status data is received from real effectors, switch state from idle to safe,
• oscillate between states safe and safe_st if not all real effectors are working properly,
• oscillate between states safe and safe_st_ok if all real effectors are working properly,
• if valid status data and valid commands are received and explicit ‘exit safe state’ command is received, oscillate between states transp and transp_st.

Additionally:

• in states safe_st, safe_st_ok and transp_st, status data is transfered from real effectors to control subsystem,
• in states safe and transp, control is calculated (safe) or transfered from control subsystem to real effectors (transp),
• switch to transparent mode (states transp and transp_st) is possible if all commands and status data are valid and all non-interrupted safe states together (safe or safe_st or safe_st_ok) were executed for at least 500 iterations.

Control subsystem velma_core_cs

FSM of velma_core_cs subsystem:

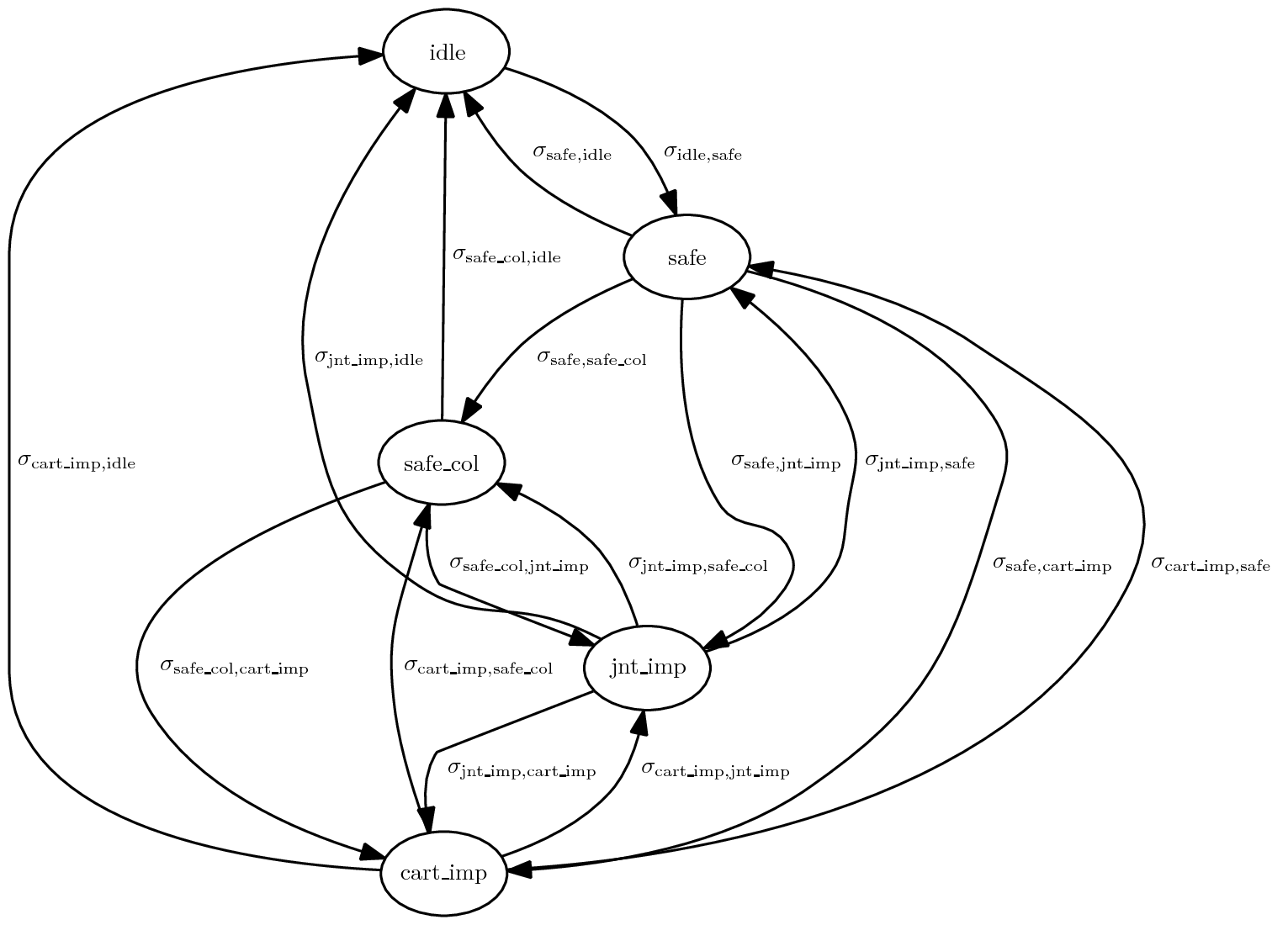
The initial state is idle and it ends when valid status is received from velma_core_ve_body and the virtual effector is not in one of its safe states (i.e. safe, safe_st, safe_st_ok or idle):

\[\scriptsize \tau_{\texttt{idle}} = \texttt{veBodyStatusValid} \wedge \neg \texttt{veBodyInSafeState}\]

The error condition for this state is never satisfied: \(\scriptsize \epsilon_{\texttt{idle}} = \texttt{FALSE}\) and the only possible state transition is \(\scriptsize \sigma_{\texttt{idle},\texttt{safe}} = \texttt{TRUE}\).

Error condition is the same for all states except idle:

\[\scriptsize \epsilon_{\texttt{safe}} = \epsilon_{\texttt{relax}} = \epsilon_{\texttt{cart_imp}} = \epsilon_{\texttt{jnt_imp}} = \neg \texttt{CURRENT_BEHAVIOR_OK} \vee \neg \texttt{veBodyStatusValid} \vee \texttt{veBodyInSafeState}\]

as well as the next state:

\[\scriptsize \sigma_{\texttt{safe},\texttt{idle}} = \sigma_{\texttt{relax},\texttt{idle}} = \sigma_{\texttt{cart_imp},\texttt{idle}} = \sigma_{\texttt{jnt_imp},\texttt{idle}} = \texttt{IN_ERROR}\]

The terminal condition and state transition conditions for state safe are:

\[\scriptsize \tau_{\texttt{safe}} = \texttt{recvOneCmd} \wedge ((( \texttt{recvCartImpCmd} \vee \texttt{recvJntImpCmd} ) \wedge \neg \texttt{inSelfCollision} ) \vee \texttt{recvRelaxCmd} ) \wedge \texttt{motorsReady}\] \[\scriptsize \sigma_{\texttt{safe},\texttt{cart_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvCartImpCmd}\] \[\scriptsize \sigma_{\texttt{safe},\texttt{jnt_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvJntImpCmd}\] \[\scriptsize \sigma_{\texttt{safe},\texttt{relax}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvRelaxCmd}\]

The terminal condition and state transition conditions for state relax are:

\[\scriptsize \tau_{\texttt{relax}} = \texttt{recvOneCmd} \wedge ( \texttt{recvCartImpCmd} \vee \texttt{recvJntImpCmd} ) \wedge \neg \texttt{inSelfCollision}\] \[\scriptsize \sigma_{\texttt{relax},\texttt{cart_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvCartImpCmd}\] \[\scriptsize \sigma_{\texttt{relax},\texttt{jnt_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvJntImpCmd}\]

The terminal condition and state transition conditions for state cart_imp are:

\[\scriptsize \tau_{\texttt{cart_imp}} = ( \texttt{recvOneCmd} \wedge ( \texttt{recvJntImpCmd} \vee \texttt{recvRelaxCmd} )) \vee \texttt{inSelfCollision}\] \[\scriptsize \sigma_{\texttt{cart_imp},\texttt{safe}} = \neg \texttt{IN_ERROR} \wedge \neg \texttt{recvOneCmd}\] \[\scriptsize \sigma_{\texttt{cart_imp},\texttt{jnt_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvOneCmd} \wedge \texttt{recvJntImpCmd}\] \[\scriptsize \sigma_{\texttt{cart_imp},\texttt{relax}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvOneCmd} \wedge \texttt{recvRelaxCmd}\]

The terminal condition and state transition conditions for state jnt_imp are:

\[\scriptsize \tau_{\texttt{jnt_imp}} = ( \texttt{recvOneCmd} \wedge ( \texttt{recvCartImpCmd} \vee \texttt{recvRelaxCmd} )) \vee \texttt{inSelfCollision}\] \[\scriptsize \sigma_{\texttt{jnt_imp},\texttt{safe}} = \neg \texttt{IN_ERROR} \wedge \neg \texttt{recvOneCmd}\] \[\scriptsize \sigma_{\texttt{jnt_imp},\texttt{cart_imp}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvOneCmd} \wedge \texttt{recvCartImpCmd}\] \[\scriptsize \sigma_{\texttt{jnt_imp},\texttt{relax}} = \neg \texttt{IN_ERROR} \wedge \texttt{recvOneCmd} \wedge \texttt{recvRelaxCmd}\]

With predicates defined as:

• \(\scriptsize \texttt{veBodyStatusValid}\) - received new status data from velma_core_ve_body,
• \(\scriptsize \texttt{veBodyInSafeState}\) - velma_core_ve_body is not in one of its safe states (i.e. safe, safe_st, safe_st_ok or idle),
• \(\scriptsize \texttt{CURRENT_BEHAVIOR_OK}\) - all component of the control subsystem are working properly (i.e. there are no errors in current transition function),
• \(\scriptsize \texttt{recvOneCmd}\) - received exactly on command from velma_ros_interface agent,
• \(\scriptsize \texttt{recvCartImpCmd}\) - received cartesian impedance command from velma_ros_interface agent,
• \(\scriptsize \texttt{recvJntImpCmd}\) - received joint impedance command from velma_ros_interface agent,
• \(\scriptsize \texttt{recvRelaxCmd}\) - received safe self collision avoidance command from velma_ros_interface agent,
• \(\scriptsize \texttt{inSelfCollision}\) - the robot is in self collision state,
• \(\scriptsize \texttt{IN_ERROR}\) - the state ends with error condition satisfied; this predicate is valid in transition conditions only.