Introduction

The main goal of the first tutorial is to learn to generate simple trajectory for a mobile robot. The robot should follow a desired trajectory, i.e. move along a straight line to a commanded target point and reach both the commanded position and orientation.

The trajectory is a straight line to the specified destination point represented as three coordinates: [x, y, phi], where x and y is the position of the robot in the XY plane, and phi is the orientation of the robot. You need to provide the youBot with a program that allows it to move along the straight-line trajectory from the starting point (any starting point is possible) to the user-defined destination point.

The commanded orientation (phi) may be reached before or after reaching the desired position (x,y). However, the orientation should change during the linear motion:

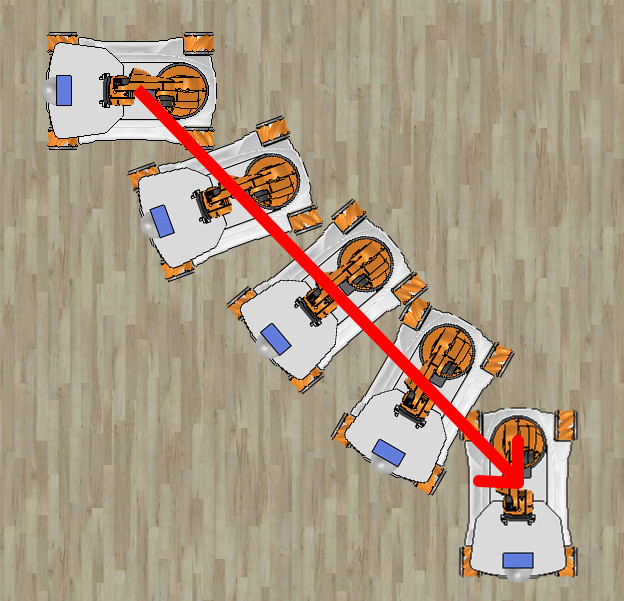
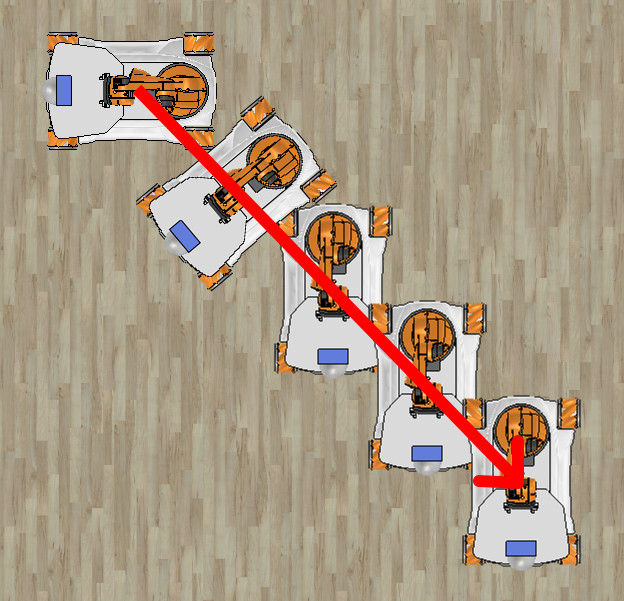
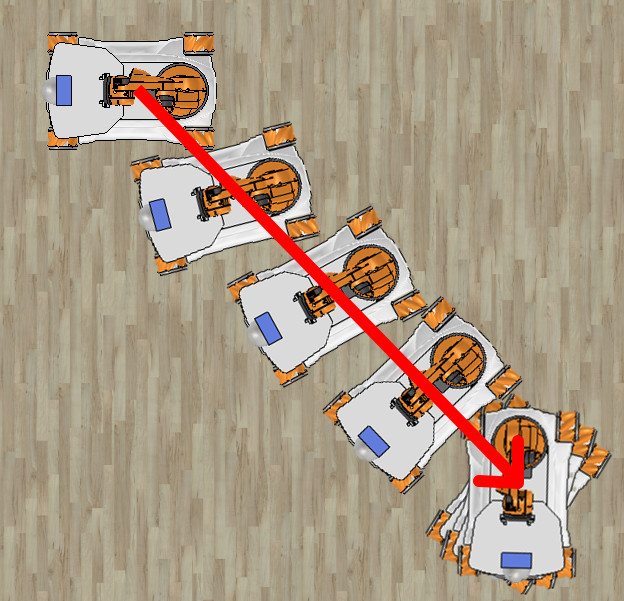
You can assume there are no obstacles and the destination point can be reached by moving on a straight line.

References

Please refer to:

• Example Task - for detailed information on principle of operation and the example scripts
• Controlling the robot - for information on moving the robot around
• Proportional regulator - for information about simple proportional regulator

The program

The script should be named solution1.m and it should be located in ~/ws_emor/emor_trs/youbot directory. The callback function for this task should be declared as:

function [forwBackVel, leftRightVel, rotVel, finish] = solution1(pts, contacts, position, orientation, varargin)
% The control loop callback function - the solution for task 1A

    % get the destination point
    if length(varargin) ~= 3,
        error('Wrong number of additional arguments: %d\n', length(varargin));
    end
    dest_x = varargin{1};
    dest_y = varargin{2};
    dest_phi = varargin{3};

    % declare the persistent variable that keeps the state of the Finite
    % State Machine (FSM)
    persistent state;
    if isempty(state),
        % the initial state of the FSM is 'init'
        state = 'init';
    end

    % initialize the robot control variables (returned by this function)
    finish = false;
    forwBackVel = 0;
    leftRightVel = 0;
    rotVel = 0;

    % TODO: manage the states of FSM
    % Write your code here...
end

To run the simulation and the control program using with the callback control function solution1 you have to run run-simulation function with proper arguments. The destination point is passed to the control program through the variable-length argument list in the run_simulation function, e.g. run_simulation(@solution1, false, 1, 2, deg2rad(90)) where the arguments are:

• solution1 is the name of the control callback function,
• false - do not display the sensor data (simulation runs faster),
• 1.0 - the x coordinate of the destination point is 1 meter,
• 2.0 - the y coordinate of the destination point is 2 meters,
• deg2rad(90) - the phi coordinate of the destination point (in radians, thus the conversion deg2rad is needed if you prefer to use degrees).

Note that the steps from the instruction in the Example Task page must be followed in order to enable the communication between Matlab and CoppeliaSim. Also, the CoppeliaSim application must be running with a proper scene!

Task requirements

• The name of the control callback function should be solution1
• The motion of the robot must be generated by P regulators with limited output - for (x,y) and for phi
• Both position and orientation must be controlled
• The robot must follow the shortest path: the straight line from the current position to the destination point
• When the destination point is reached, the function must return finish=true to stop the control program
• You can use the environment file ~/emor_trs/youbot/vrep_env/exercise01.ttt in CoppeliaSim simulation.

Please Note that the regulator of angular velocity and regulators of linear velocities are independent, so the following cases are acceptable:

• the robot reaches the desired orientation before reaching the desired point (as in the central picture)
• the robot reaches the desired point before reaching the desired orientation (as in the picture on the right)

Still, at the end, both desired orientation and position must be reached within some tolerance, e.g. 0.05 meters for position and 5 degrees for orientation.

Grading

You can get 5 points, including:

• x, y and phi coordinates regulation (proportional with limited output)
• using reference frames transformations
• proper stop condition and clean exit (if all previous requirements are met)

A complete solution for a task is the source code and a report.

Please refer to the Schedule page for consultation dates and deadlines.